1. What is a Pairwise testing?
Pairwise testing is a technique for creating testing data sets from the complete input data sets to reduce the number of test cases.
This definition could thus be formulated as follows: It is a generation of data sets in which every testing value of each of the variables combines at least once with each value of other variables.
The main objectives of pairwise testing:
- to remove unnecessary testing;
- to create an adequate test coverage;
- to detect the greatest possible number of defects using the minimal number of tests.
Let us consider the basic idea of pairwise testing through the following examples.
Example 1
Let us take the system with 3 variables: A, B, and C that can take the values «Yes» or «No.» The maximum number of combinations of these variables is 8. However during pairwise testing, 4 combinations are enough since all possible pairs are counted. (A and B, B and C, A and C):
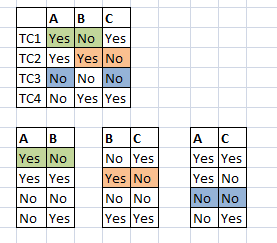
Example 2
Let’s assume some value for a person (for example, taxes) is calculated based on gender, age, and presence of children. So, we get 3 input variables, for every of which we should choose any possible value for the test.
For example, let’s take gender - male or female; age – under 25, from 25 to 60, above 60; the presence of children – yes or no. To check the validity of calculations, we can run through all the value combinations of all the variables:
| № | Gender | Age | Children |
| 1 | male | under 25 | no |
| 2 | female | under 25 | no |
| 3 | male | 25-60 | no |
| 4 | female | 25-60 | no |
| 5 | male | over 60 | no |
| 6 | female | over 60 | no |
| 7 | male | under 25 | yes |
| 8 | female | under 25 | yes |
| 9 | male | 25-60 | yes |
| 10 | female | 25-60 | yes |
| 11 | male | over 60 | yes |
| 12 | female | over 60 | yes |
There is also another way to resolve it. It is not necessary to check the combination of every value but ensure that all unique pairs are verified. For example, from the point of view of gender and age parameters, we need to ensure that we check the man under 25, the man between 25 and 60, the man above 60, and also the woman under 25, between 25 and 60 and above 60. We can apply the same way to other pairs of variables. Hence, we can obtain much fewer value sets (there are all pairs of values, sometimes twice)
| № | Gender | Age | Children |
| 1 | male | under 25 | no |
| 2 | female | under 25 | yes |
| 3 | male | 25-60 | yes |
| 4 | female | 25-60 | no |
| 5 | male | over 60 | no |
| 6 | female | over 60 | yes |
Example 3
There are two browsers: Opera and Firefox, and two operation systems: Windows and Linux. There is nothing to reduce here as they can be formed in four configurations.
| № | Browser | OS |
| 1 | Opera | Windows |
| 2 | Firefox | Linux |
| 3 | Opera | Linux |
| 4 | Firefox | Windows |
Let us assume there is a website in two languages: Russian and English. As an experiment, multiply these 4 configurations by 2, that is to say, check every previous configuration with two languages. However, actually, we do not need to do it. If we use pairwise testing, we can receive 4 configurations instead of 8:
| № | Browser | OS | Language |
| 1 | Opera | Windows | RU |
| 2 | Firefox | Linux | RU |
| 3 | Opera | Linux | EN |
| 4 | Firefox | Windows | EN |
Furthermore, the website can use MySQL, Oracle, and MSSQL as databases. Using pairwise testing, we can get 7 configurations (rather than 12 – previous 4х3, let alone 24 = 2х2х2х3). But it is worth considering whether it is essential to check every database in combination with other variables. What is important to test is how every database works with each language. Therefore, by imposing the restrictions, we will get 6 configurations instead of 7 (3 databases х 2 languages):
| № | Browser | OS | Language | Database |
| 1 | Opera | Windows | RU | MySQL |
| 2 | Firefox | Linux | EN | MySQL |
| 3 | Opera | Linux | EN | MSSQL |
| 4 | Firefox | Windows | RU | MSSQL |
| 5 | Opera | Linux | RU | Oracle |
| 6 | Firefox | Windows | EN | Oracle |
Example 4
The basic principle of pairwise testing is that there is no need to do the complete factorial experiment (going through all configurations where all the values combine). And it is also impossible due to the lack of resources.
Consequently, it is enough to check how the system works when every value of every variable combines with another value of every variable at least once.
Suppose there can be a defect due to the variable combinations:
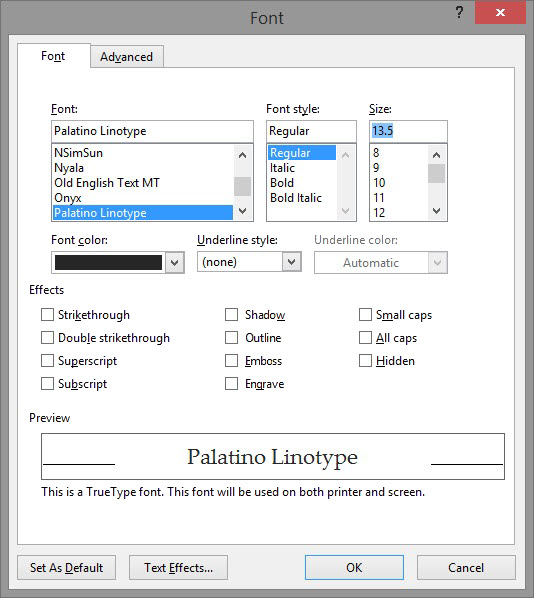
How many tests should be done to cover all the values?
We need to take the following variables and their values:
| Parameter | Value 1 | Value 2 | Value 3 | Value 4 |
| Font | TT | Arial | ||
| Style | Regular | Italic | Bold | Bold Italic |
| Size | min | normal | max | |
| Color | black | white | red | |
| Underline style | none | words only | other | |
| Strikethrough | on | off | ||
| Double Strikethrough | on | off | ||
| Superscript | on | off | ||
| Subscript | on | off | ||
| Shadow | on | off | ||
| Outline | on | off | ||
| Emboss | on | off | ||
| Engrave | on | off | ||
| Small caps | on | off | ||
| All caps | on | off | ||
| Hidden | on | off |
If we take all the accessible combinations and multiply all the numbers of values of each variable, we will get this number of checks:
2 * 4 * 3 * 3 * 3 * 2^11 = 442 368.
The final verification spreadsheet:
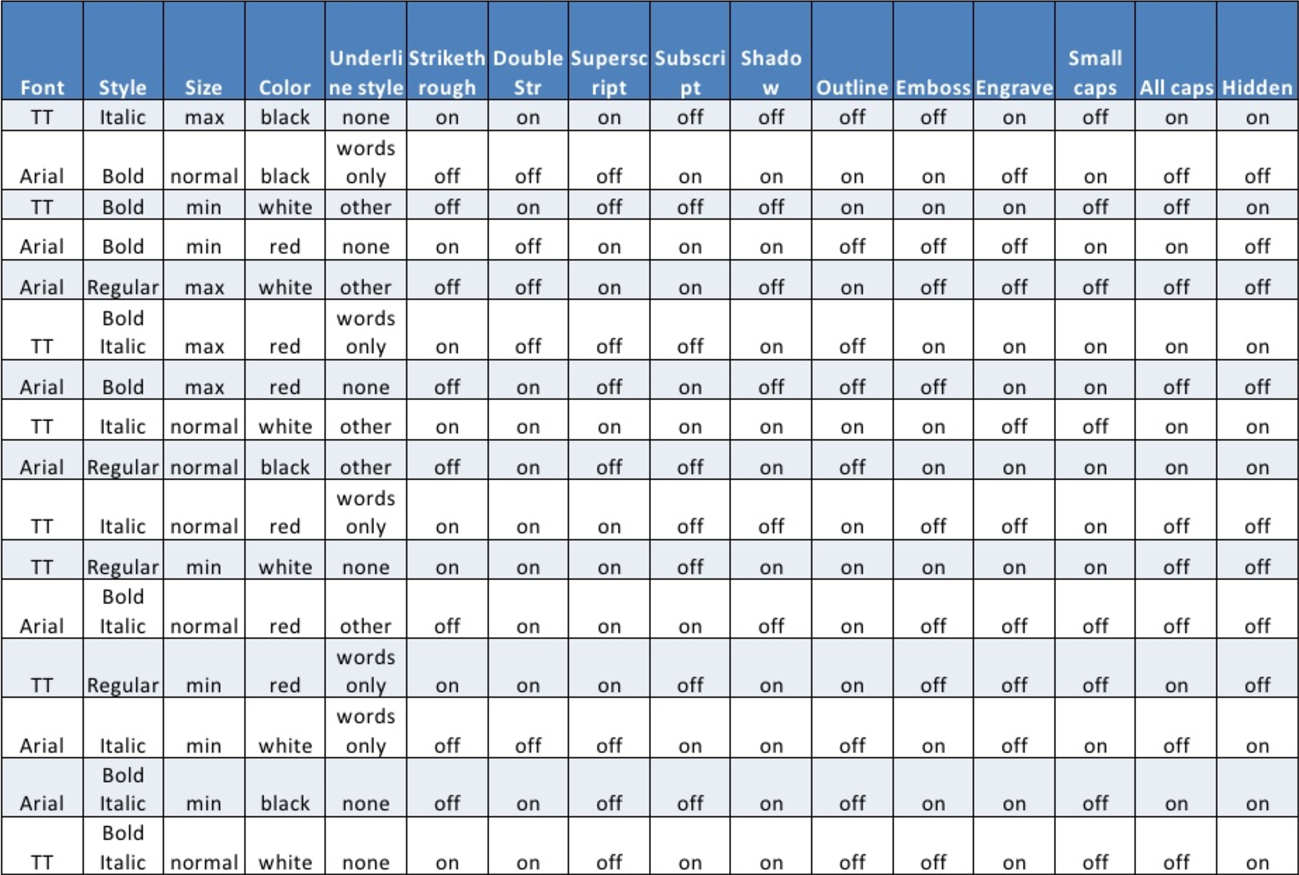
Therefore, the pairwise technique makes it possible to reduce the number of tests significantly.
2. Tools
Compiling the required value combinations is not an easy task sometimes. Luckily, there are many tools of different qualities to smooth things down for it.
In the given materials, we will consider such a tool as PICT (Pairwise Independent Combinatorial Testing – the pairwise testing tool by Microsoft).
PICT allows us to generate a compact set of variables data, which constitutes test scenarios for full combinatorial parameter coverage.
Let’s consider how the program works. First of all, PICT is launched from a command line.
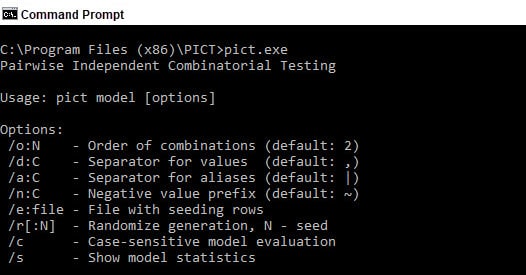
As an input, the program accepts a simple test file, called the model, with variables and their values, and as an output, we receive generated test scenarios.
Let’s see the program work in example 2 above. There are parameters and their values such as: gender - male or female; age – under 25, from 25 to 60, above 60; the presence of children – yes or no. If we go through all the possible values, there will be 12 scenarios. So let’s make the model and see the result the program will deliver.
Model:
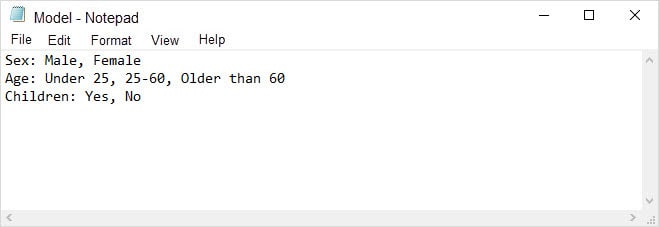
We use the model in PICT and receive 6 testing scenarios instead of 12:
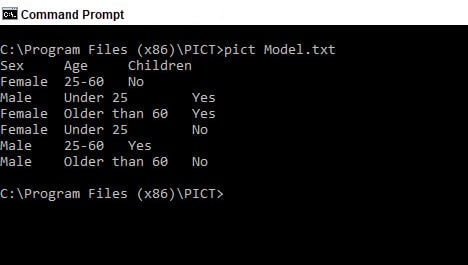
The difference is not significant, but it will be with the increasing number of testing variables or their values.
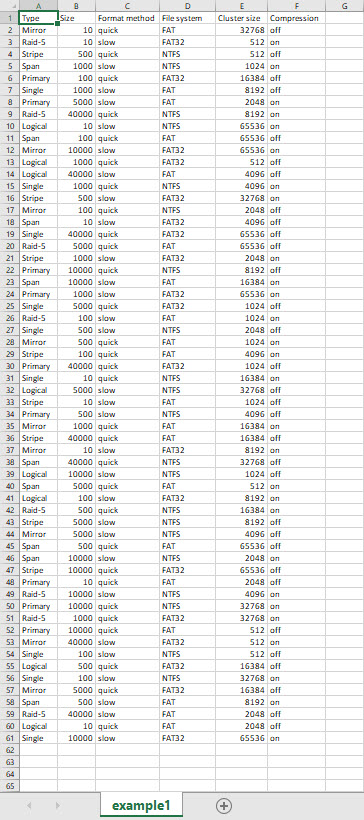
Imagine there are testing parameters related to the creating sections testing on the hard drive (the example comes from the PICT manual):
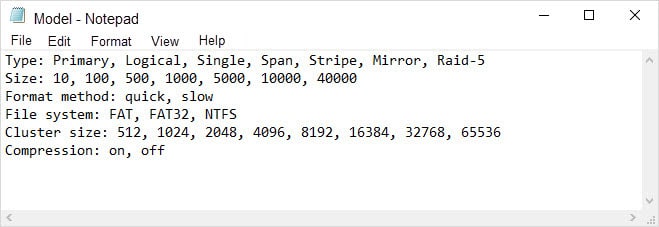
It is not difficult to count the number of available checkings and multiply every value.
7 * 7 * 2 * 3 * 8 * 2 = 4704
In this case, it will not be easy to perform the testing in a reasonable amount of time.The research indicates that testing every possible pair provides high-quality coverage, and the number of tests is within reasonable limits.
For example, {Primary, FAT} this is one pair and {10, slow} is another; one test case can cover multiple pairs.
For the set of above mentioned parameters, PICT creates only 60 of them.
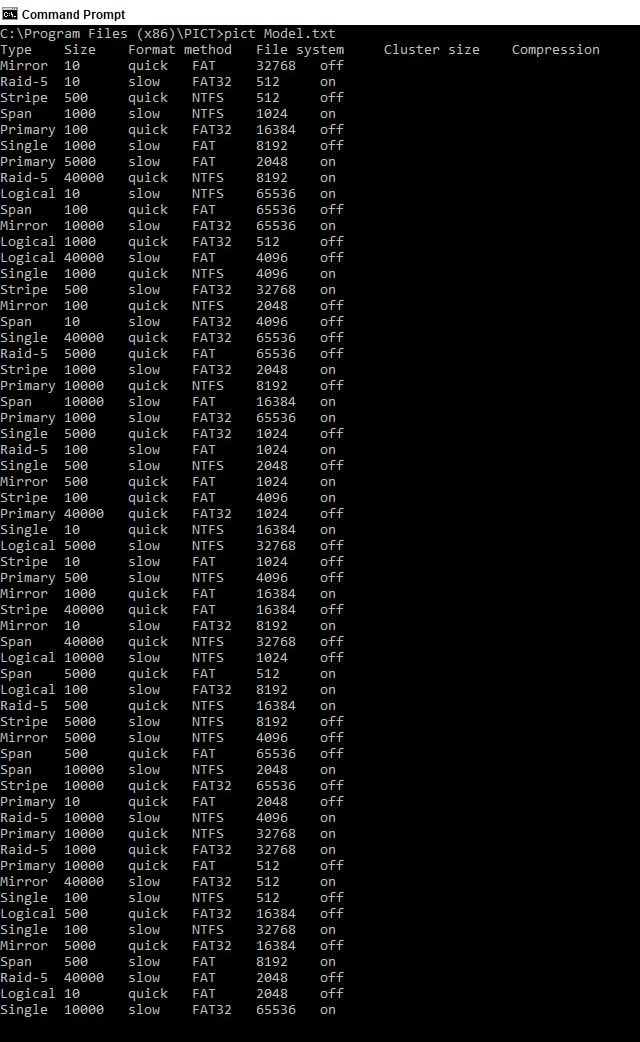
Moreover, instead of the usual outputting into the console, we can use the direct extraction and saving text cases in MS Excel:

As a result, the following file will be created:
The most interesting are the opportunities provided by PICT for the similar scenario generation.
All of them are thoroughly considered in the user manual. There are some of them below:
- It is possible to indicate the order of values groups. By default, order 2 is used, and combinations of value pairs are created (and that is what we call pairwise testing.) But we can also indicate, for example, 3, and in that case, triplets will be used and not pairs. In the simple model, the maximal order of value groups equals the number of variables, which makes sets of multiple options.
- We may group variables as sub-models and set them in a separate order to make combinations. It is required when the combinations of certain variables must be tested more thoroughly or combined separately from other parameters.
- It is possible to create conditions and restrictions. For example, it is possible to indicate that one of the variables will take the value only when some other variables take specific values. Thus, it allows reducing unnecessary checks.
- It is possible to indicate invalid variable values during the creation of combinations for negative tests.
- Using weighting factors, we can make the program prioritize specific values during the generation of combinations.
- We can use the minimization option (to reload the program several times using the shortened test cases).
In conclusion, we want to say that PICT is a very convenient tool for the quick creation of a set of test data combinations, especially when there is a large number of barely connected variables (It allows not to test all possible options). However, it is necessary to create thoroughly a specified model for the test coverage to be satisfactory.
3. When and where do we use the Pairwise technique?
The method is effective only in the final stages of development or when supplementing with the principal functional tests.
For example: if we do the configuration testing, before using the pairwise technique, we need to ensure that the principal scenario functions on all operating systems with defaulting parameters (perform the
Smoke testing or Build Verification Test It will significantly facilitate the localization of future bugs since, in one test, there are many parameters with non-default values during pairwise testing, every one of which might cause defects, and in this case, localizing them is not easy.In the event of failure of build testing, we should refuse to use the pairwise technique as many tests will fail, as the exception of at least one test will usually cause the loss of a few pairs. In that case, it does not make sense to use this method.
That is why we should use this method only with a steady functional after the effectiveness of existing tests is exhausted.
Therefore, the Pairwise technique is a particular method of optimizing the design of test cases.
The technique's central concept is not to check all combinations of the values but to verify all pairs of these values.



